What Is 5 To The Fifth Power
Arias News
Mar 29, 2025 · 5 min read
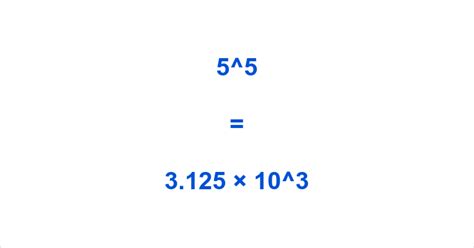
Table of Contents
What is 5 to the Fifth Power? A Deep Dive into Exponentiation
Understanding exponentiation, or raising a number to a power, is a fundamental concept in mathematics. This article will delve into the specific calculation of 5 to the fifth power (5⁵), exploring its meaning, calculation methods, applications, and related mathematical concepts. We'll go beyond simply stating the answer and explore the broader implications of this seemingly simple mathematical operation.
Understanding Exponentiation
Before tackling 5⁵, let's solidify our understanding of exponentiation. Exponentiation is a mathematical operation written as bⁿ, where 'b' is the base and 'n' is the exponent or power. It signifies repeated multiplication of the base by itself, 'n' number of times.
For example:
- 2³ = 2 × 2 × 2 = 8 (2 is the base, 3 is the exponent)
- 10² = 10 × 10 = 100 (10 is the base, 2 is the exponent)
In our case, we're dealing with 5⁵, meaning:
5⁵ = 5 × 5 × 5 × 5 × 5
Calculating 5 to the Fifth Power
The most straightforward way to calculate 5⁵ is through repeated multiplication:
- Step 1: 5 × 5 = 25
- Step 2: 25 × 5 = 125
- Step 3: 125 × 5 = 625
- Step 4: 625 × 5 = 3125
Therefore, 5 to the fifth power is 3125.
Beyond Simple Multiplication: Exploring Alternative Methods
While repeated multiplication is effective for smaller exponents, it can become cumbersome for larger numbers. Let's explore alternative approaches:
Using a Calculator
Modern calculators readily handle exponentiation. Most calculators have a button (often denoted as xʸ or ^) specifically for this operation. Simply input 5, press the exponentiation button, then input 5, and press equals (=). The calculator will directly output the result: 3125.
Logarithms and Exponentials
Logarithms and exponentials are inverse functions. While less intuitive for this specific problem, understanding their relationship provides a powerful tool for solving more complex exponential equations. For instance, if we had an equation like x⁵ = 3125, we could use logarithms (base 5) to solve for x. However, for this simple case, direct multiplication remains the most efficient approach.
Programming and Computation
Programming languages offer built-in functions for exponentiation. In Python, for instance, you would use the ** operator: 5 ** 5. This provides a computationally efficient way to calculate powers, especially when dealing with very large numbers or repetitive calculations.
Applications of Exponentiation: Real-World Examples
Exponentiation isn't just an abstract mathematical concept; it has numerous practical applications across various fields:
Compound Interest
In finance, compound interest calculations rely heavily on exponentiation. The formula for compound interest is: A = P (1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The (1 + r/n)^(nt) part of the formula shows the power of exponentiation in determining the growth of an investment over time.
Population Growth
Exponential growth models are frequently used to describe population growth (of humans, animals, bacteria, etc.). If a population grows at a constant rate, its size after a certain period can be calculated using an exponential function.
Radioactive Decay
Conversely, radioactive decay follows an exponential decay model. The amount of a radioactive substance remaining after a certain time can be determined using an exponential function. This is crucial in fields like nuclear physics and medicine.
Computer Science and Data Structures
Exponentiation appears in algorithms related to data structures like trees and graphs. The time complexity of some algorithms is expressed using exponential notation, indicating how the runtime scales with the input size. Understanding exponentiation is therefore essential for optimizing algorithm performance.
Expanding Our Understanding: Exploring Related Concepts
Understanding 5⁵ provides a foundation for exploring related mathematical concepts:
Higher Powers of 5
We've calculated 5⁵, but what about 5⁶, 5⁷, and so on? These higher powers of 5 can be calculated using the same methods discussed above: repeated multiplication, calculators, or programming. Observe the pattern in the results to gain further insight into exponential growth.
Powers of Other Numbers
The principles of exponentiation apply to any base, not just 5. Experiment with calculating powers of different numbers (both integers and decimals) to enhance your understanding.
Negative Exponents
Negative exponents indicate reciprocals. For example, 5⁻¹ = 1/5 = 0.2, and 5⁻² = 1/5² = 1/25 = 0.04. Understanding negative exponents is crucial for solving various mathematical problems.
Fractional Exponents
Fractional exponents represent roots. For instance, 5¹/² represents the square root of 5, and 5³/² represents the square root of 5³ (or the cube of the square root of 5).
Complex Numbers and Exponentiation
Exponentiation can be extended to complex numbers, introducing the fascinating world of complex exponentials, with applications in areas like signal processing and quantum mechanics.
Conclusion: The Significance of 5 to the Fifth Power
While the calculation of 5⁵ might seem simple at first glance, it serves as a gateway to a richer understanding of exponentiation. By exploring different calculation methods, real-world applications, and related mathematical concepts, we've deepened our understanding of this fundamental mathematical operation. The seemingly straightforward result of 3125 reveals the power and significance of exponential growth and decay, underpinning various phenomena across numerous fields. This foundational understanding is crucial for tackling more complex mathematical problems and appreciating the intricate workings of the world around us.
Latest Posts
Latest Posts
-
Will A Queen Mattress Fit In A Full Bed Frame
Apr 01, 2025
-
How Many Cheese Balls Are In A Container
Apr 01, 2025
-
How Many Gallons Is 35 Lbs Of Oil
Apr 01, 2025
-
What Best Describes The 3 Major Threats In Air Transport
Apr 01, 2025
-
Lowest Common Factor Of 24 And 30
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The Fifth Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
