What Is A Triangle With No Equal Sides
Arias News
Mar 30, 2025 · 6 min read
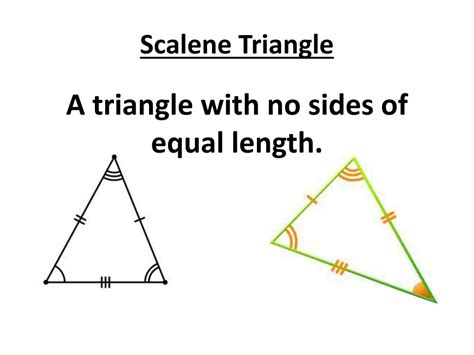
Table of Contents
What is a Triangle with No Equal Sides? A Deep Dive into Scalene Triangles
A triangle, the most fundamental polygon, is a closed two-dimensional figure defined by three straight lines intersecting at three points called vertices. While triangles can be categorized in various ways based on their angles (acute, obtuse, right), another crucial classification hinges on the lengths of their sides. This article delves into the fascinating world of scalene triangles, triangles with no equal sides. We'll explore their properties, characteristics, uniqueness, and their significance in various fields.
Defining a Scalene Triangle: The Essence of Inequality
A scalene triangle is a triangle where all three sides have different lengths. This inherent inequality distinguishes it from other types of triangles like equilateral (all sides equal) and isosceles (two sides equal). The lack of symmetry in side lengths introduces unique geometric properties and challenges that make scalene triangles a captivating subject in geometry and related disciplines.
This fundamental characteristic – the unequal length of sides – directly impacts other aspects of the triangle, including its angles. Unlike equilateral triangles with 60-degree angles or isosceles triangles with at least two equal angles, scalene triangles possess three unequal angles. This absence of symmetry makes them the most diverse and versatile type of triangle.
Properties of Scalene Triangles: A Unique Geometric Identity
Several key properties define scalene triangles and differentiate them from their more symmetrical counterparts:
- Three Unequal Sides: This is the defining characteristic. No two sides share the same length.
- Three Unequal Angles: The lengths of the sides directly correspond to the magnitude of the opposite angles. The longest side always opposes the largest angle, and the shortest side opposes the smallest angle. This relationship is governed by the Law of Sines and the Law of Cosines, which are fundamental tools in solving scalene triangle problems.
- No Lines of Symmetry: Unlike isosceles triangles with a line of symmetry through the apex and the midpoint of the base, scalene triangles lack any lines of symmetry. This lack of symmetry makes them visually distinct and less predictable in their geometric behavior.
- Area Calculation: The area of a scalene triangle can be calculated using Heron's formula, a powerful tool that utilizes the lengths of all three sides to determine the area. This formula is especially useful when dealing with triangles where the height isn't easily calculable. Alternatively, the standard formula (1/2 * base * height) can also be applied, but finding the height might require additional calculations using trigonometric functions.
- Circumcenter and Incenter: The circumcenter (the center of the circumscribed circle) and incenter (the center of the inscribed circle) are not coincident in scalene triangles, unlike in equilateral triangles. Their positions are determined by the unique geometric relationships between the sides and angles.
Solving Scalene Triangles: Applying Trigonometric Principles
Solving a scalene triangle involves determining the unknown sides and angles given certain information. This is where trigonometry plays a vital role. Two essential laws are crucial for these calculations:
The Law of Sines:
This law establishes a relationship between the angles and sides of any triangle, including scalene triangles. It states:
a/sin(A) = b/sin(B) = c/sin(C)
where:
- a, b, and c are the lengths of the sides opposite angles A, B, and C respectively.
This law is incredibly useful when you know two angles and one side (AAS or ASA) or two sides and one non-included angle (SSA). However, the SSA case can sometimes lead to ambiguous solutions (two possible triangles) which requires careful consideration.
The Law of Cosines:
This law provides a powerful alternative for solving triangles, especially when dealing with three sides (SSS) or two sides and the included angle (SAS). It states:
a² = b² + c² - 2bc*cos(A)
Similar equations can be derived for b² and c². This law directly incorporates the cosine of an angle, making it a versatile tool for solving various types of triangle problems.
Real-World Applications of Scalene Triangles: Beyond the Textbook
While often considered a relatively simple geometric concept, scalene triangles have significant applications in diverse fields:
Engineering and Architecture:
- Structural Design: Engineers frequently use scalene triangles in the design of bridges, buildings, and other structures. Their unique properties allow for the distribution of forces and stresses in a way that optimizes stability and strength.
- Truss Structures: Many truss systems, used in bridges and roofs, rely on scalene triangles to form a strong and lightweight framework. The varying side lengths provide specific strength and stability characteristics based on the load distribution.
- Surveying and Mapping: Scalene triangles are fundamental tools in surveying and mapping for determining distances and areas of land. Their versatility makes them adaptable to various terrains and configurations.
Computer Graphics and Game Development:
- Polygon Modeling: Scalene triangles are the building blocks of many 3D models in computer graphics. Their irregular shapes allow for the creation of complex and realistic surfaces and objects. This is essential in gaming, animation, and architectural visualization.
- Texture Mapping: The irregular shapes are utilized to create textures and lighting effects on 3D models, adding realism and detail. The varying sizes and shapes contribute to the overall visual fidelity.
- Collision Detection: In game physics engines, scalene triangles are frequently used for collision detection between objects. Their irregular shapes accurately represent the complexity of real-world objects.
Navigation and GPS:
- Triangulation: The principle of triangulation uses the measurements of angles from different locations to pinpoint the location of a point. This method often involves scalene triangles due to the irregular distances and angles involved.
- GPS Systems: While often simplified in explanations, the underlying calculations involve complex geometrical relationships, frequently including the application of principles related to scalene triangles.
Art and Design:
- Artistic Composition: Artists unconsciously or consciously use the visual appeal of scalene triangles to create dynamic and visually interesting compositions. The asymmetry creates a sense of movement and energy.
- Architectural Design (Aesthetic Aspects): The use of scalene triangles in architectural design isn't solely functional. The varying side lengths can contribute to aesthetic qualities, creating a unique visual impact.
Beyond the Basics: Advanced Concepts and Explorations
The world of scalene triangles extends beyond basic geometric properties and solving techniques. Several advanced concepts further enhance our understanding of their unique characteristics:
Solving Scalene Triangles with Ambiguous Cases:
The SSA (Side-Side-Angle) case in triangle solving can be ambiguous, meaning there might be two possible solutions. Understanding the conditions that lead to ambiguity and utilizing trigonometric tools to determine the correct solution is crucial.
Area Calculation Using Determinants:
The area of a scalene triangle can also be efficiently calculated using determinants involving the coordinates of its vertices. This method offers an alternative approach, particularly useful in coordinate geometry applications.
Scalene Triangles in Higher Dimensions:
The concept of scalene triangles can be extended to higher dimensions, leading to more complex geometric figures with similar properties but in a three-dimensional or multi-dimensional space.
Conclusion: The Enduring Significance of Scalene Triangles
Scalene triangles, despite their seemingly simple definition, possess a rich tapestry of geometric properties and applications. Their inherent asymmetry leads to unique challenges and opportunities in solving problems and modeling real-world phenomena. From the foundations of trigonometry to advanced applications in engineering and computer graphics, the study of scalene triangles provides a solid foundation for understanding more complex geometric concepts and their practical implications. Their versatility and ubiquity underscore their enduring importance across diverse scientific and artistic disciplines. The exploration of scalene triangles continues to yield new insights and applications, solidifying their position as a cornerstone of geometric understanding.
Latest Posts
Latest Posts
-
How Far Is Mt Pilot From Mayberry
Apr 01, 2025
-
How Far Is 200 Metres To Walk
Apr 01, 2025
-
Is Crushed Red Pepper The Same As Chili Flakes
Apr 01, 2025
-
A N Is The Hardware And Software Connecting Electronic Devices
Apr 01, 2025
-
How Many Right Angles Does A Square Have
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Triangle With No Equal Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
