What Is Half Of A Quarter Of 400
Arias News
May 08, 2025 · 5 min read
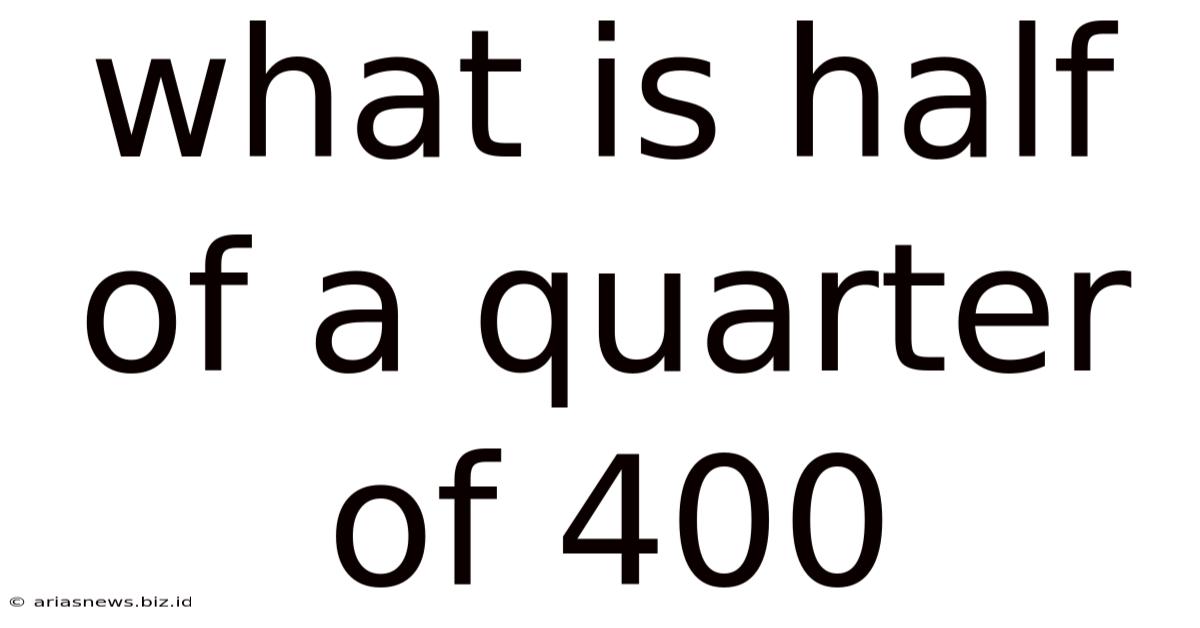
Table of Contents
What is Half of a Quarter of 400? A Deep Dive into Fractions and Problem Solving
This seemingly simple question, "What is half of a quarter of 400?", opens a door to exploring fundamental mathematical concepts, problem-solving strategies, and even the nuances of language interpretation. While the answer itself is straightforward, the journey to finding it offers valuable insights into fractions, percentages, and the importance of clear, step-by-step reasoning. This article will not only solve the problem but also delve into the underlying mathematical principles and provide practical applications to solidify your understanding.
Understanding Fractions: The Building Blocks of the Problem
Before tackling the problem directly, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, ½ (one-half) means a whole is divided into two equal parts, and we are considering one of those parts. Similarly, ¼ (one-quarter) signifies that a whole is divided into four equal parts, and we are focusing on one of them.
Deconstructing the Problem: A Step-by-Step Approach
The problem "What is half of a quarter of 400?" can be broken down into smaller, more manageable steps:
-
Find a quarter of 400: This involves dividing 400 by 4. Mathematically, this is represented as (¼) * 400 = 400 / 4 = 100.
-
Find half of the result: Now that we know a quarter of 400 is 100, we need to find half of 100. This is calculated as (½) * 100 = 100 / 2 = 50.
Therefore, half of a quarter of 400 is $\boxed{50}$.
Expanding the Understanding: Percentages and Decimal Equivalents
Fractions are intrinsically linked to percentages and decimals. Understanding these interrelationships can provide alternative approaches to solving similar problems.
Converting Fractions to Percentages:
A percentage is a fraction expressed as a part of 100. To convert a fraction to a percentage, multiply the fraction by 100%.
- ¼ (one-quarter) = (¼) * 100% = 25%
- ½ (one-half) = (½) * 100% = 50%
Thus, the problem can be rephrased as: "What is 50% of 25% of 400?"
Converting Fractions to Decimals:
A decimal is another way to represent a fraction, using a base-ten system. To convert a fraction to a decimal, divide the numerator by the denominator.
- ¼ (one-quarter) = 1 ÷ 4 = 0.25
- ½ (one-half) = 1 ÷ 2 = 0.5
The problem can also be expressed as: "What is 0.5 of 0.25 of 400?" Solving this using decimal multiplication yields the same result: 0.5 * 0.25 * 400 = 50.
Real-World Applications: Putting Fractions into Practice
The principles of fractions are not confined to abstract mathematical exercises. They are fundamental to numerous real-world scenarios, including:
-
Cooking and Baking: Recipes frequently use fractions (e.g., ½ cup of sugar, ¼ teaspoon of salt). Understanding fractions is essential for accurate measurements and consistent results.
-
Construction and Engineering: Precise measurements and calculations are vital in construction and engineering. Fractions are used extensively in blueprint reading, material calculations, and structural designs.
-
Finance and Budgeting: Managing finances involves understanding fractions and percentages. Calculating interest rates, discounts, and tax deductions all rely on fractional calculations.
-
Data Analysis: Fractions and percentages are extensively used to represent proportions and trends in data analysis and statistics. Understanding these concepts is critical for interpreting charts, graphs, and statistical reports.
-
Time Management: Understanding fractions of an hour (e.g., ½ hour, ¼ hour) is essential for effective time management and scheduling.
Beyond the Basics: Advanced Fraction Operations
While the initial problem was relatively simple, understanding fractions extends to more complex operations like addition, subtraction, multiplication, and division of fractions.
Addition and Subtraction of Fractions:
Adding and subtracting fractions requires finding a common denominator – a number that is a multiple of both denominators. For instance, to add ½ and ¼, we find the common denominator (4) and rewrite the fractions:
½ + ¼ = (2/4) + (1/4) = 3/4
Multiplication and Division of Fractions:
Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions is equivalent to multiplying by the reciprocal of the second fraction (inverting the numerator and denominator).
- (½) * (¼) = (11) / (24) = ⅛
- (½) ÷ (¼) = (½) * (4/1) = 2
Problem-Solving Strategies: Cultivating Mathematical Thinking
Successfully solving mathematical problems, regardless of their complexity, involves more than just knowing the formulas. It requires a strategic approach:
-
Understand the Problem: Carefully read and understand the problem statement. Identify the key information and what is being asked.
-
Develop a Plan: Outline a step-by-step plan to solve the problem. This might involve using diagrams, formulas, or breaking the problem into smaller parts.
-
Execute the Plan: Implement your plan systematically, performing the necessary calculations accurately.
-
Check Your Answer: Review your answer to ensure it makes sense in the context of the problem. Consider checking your work using a different method or approach.
-
Reflect and Learn: Once you have solved the problem, reflect on the process. What strategies did you use? What could you have done differently? Learning from your experiences enhances your problem-solving skills.
Conclusion: Mastering Fractions for a Brighter Future
This in-depth exploration of "What is half of a quarter of 400?" has revealed that the answer (50) is merely the tip of the iceberg. Understanding fractions, percentages, and decimals, along with effective problem-solving strategies, are crucial skills applicable across various fields. By mastering these fundamental mathematical concepts, you equip yourself with powerful tools for navigating the complexities of the real world, making informed decisions, and unlocking a deeper understanding of the universe around us. The journey of learning is ongoing, and continued exploration will only strengthen your mathematical abilities and enhance your problem-solving capabilities. Remember to practice consistently to solidify your understanding and build confidence in your mathematical skills. The more you practice, the easier and more intuitive these concepts will become.
Latest Posts
Latest Posts
-
5 Less Than The Product Of 3 And A Number
May 11, 2025
-
A Correlation Coefficient Of 1 36 Would Be
May 11, 2025
-
4 Right Angles And 4 Equal Sides
May 11, 2025
-
Is Melting An Ice Cube A Physical Or Chemical Change
May 11, 2025
-
What Does It Mean When A Wishbone Breaks Evenly
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of A Quarter Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.