What Is The Gcf Of 28 And 49
Arias News
May 11, 2025 · 6 min read
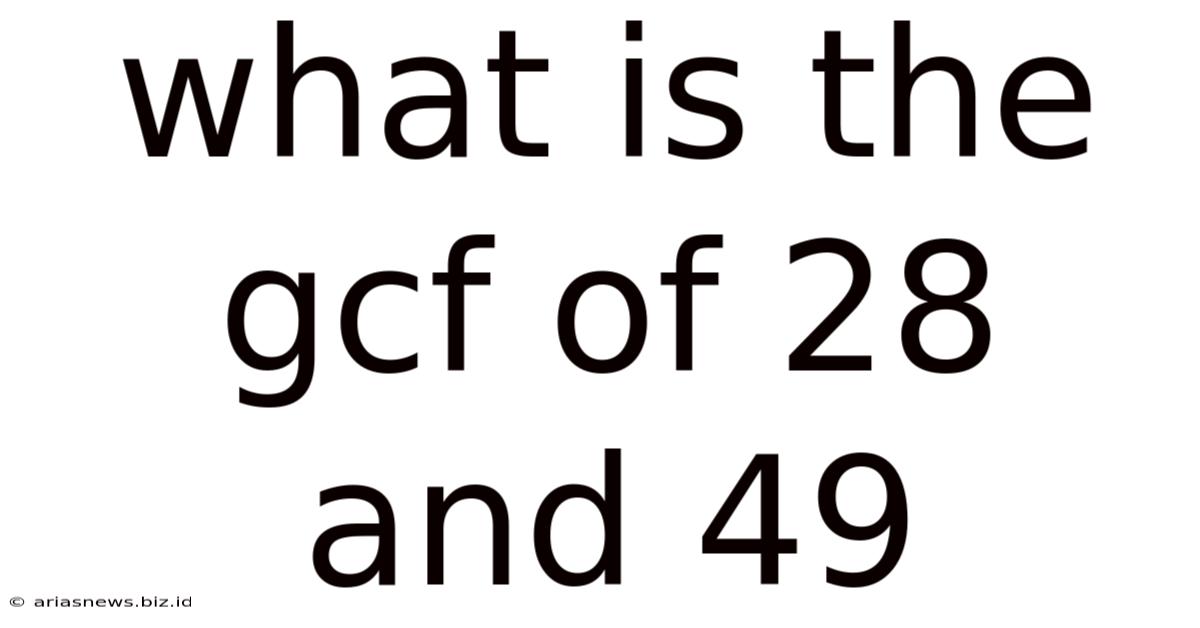
Table of Contents
What is the GCF of 28 and 49? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it can be surprisingly insightful. This comprehensive guide will not only answer the question, "What is the GCF of 28 and 49?" but also delve deep into the world of GCFs, exploring various approaches and their applications in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding number theory.
Why is finding the GCF important?
The GCF is a crucial concept in mathematics because it allows us to:
-
Simplify fractions: Reducing fractions to their simplest form involves dividing both the numerator and denominator by their GCF. For example, the fraction 28/49 can be simplified using the GCF of 28 and 49.
-
Solve algebraic equations: GCF plays a vital role in factoring polynomials, a critical step in solving many algebraic equations.
-
Understand number relationships: Finding the GCF helps us understand the relationships between numbers and identify common divisors. This is essential in various areas of mathematics, including number theory and cryptography.
-
Real-world applications: GCF finds applications in various real-world scenarios, such as dividing objects into equal groups, arranging items in a grid, or determining the size of the largest square tile that can be used to cover a rectangular floor without any gaps or overlaps.
Methods for Finding the GCF of 28 and 49
There are several effective methods to determine the greatest common factor of two numbers. Let's explore the most common ones, applying them to find the GCF of 28 and 49.
1. Listing Factors Method
This straightforward method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 28: 1, 2, 4, 7, 14, 28 Factors of 49: 1, 7, 49
Comparing the two lists, we see that the common factors are 1 and 7. The largest of these is 7.
Therefore, the GCF of 28 and 49 is 7.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then multiplying the common prime factors raised to their lowest powers.
Prime factorization of 28: 2 x 2 x 7 = 2² x 7 Prime factorization of 49: 7 x 7 = 7²
The only common prime factor is 7. The lowest power of 7 present in both factorizations is 7¹.
Therefore, the GCF of 28 and 49 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
- Divide the larger number (49) by the smaller number (28): 49 ÷ 28 = 1 with a remainder of 21.
- Replace the larger number with the remainder: Now we find the GCF of 28 and 21.
- Divide the larger number (28) by the smaller number (21): 28 ÷ 21 = 1 with a remainder of 7.
- Replace the larger number with the remainder: Now we find the GCF of 21 and 7.
- Divide the larger number (21) by the smaller number (7): 21 ÷ 7 = 3 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 7.
Applications of GCF in Real-World Scenarios
The concept of GCF isn't confined to theoretical mathematics; it has practical applications in various everyday situations.
1. Dividing Objects into Equal Groups
Imagine you have 28 apples and 49 oranges, and you want to divide them into the largest possible equal groups, such that each group contains the same number of apples and oranges. The GCF of 28 and 49 (which is 7) determines that you can create 7 equal groups, each containing 4 apples and 7 oranges.
2. Arranging Items in a Grid
Suppose you're arranging 28 red squares and 49 blue squares in a rectangular grid. The dimensions of the largest possible square grid that can accommodate both colors of squares without any gaps are determined by the GCF. Since the GCF is 7, the largest square grid would be 7 x 7.
3. Cutting Fabric or Paper
Imagine you have two pieces of fabric, one measuring 28 inches and the other measuring 49 inches. You want to cut them into identical smaller squares of the largest possible size. The GCF (7 inches) determines the size of the largest square you can cut without any waste.
4. Simplifying Ratios and Fractions
GCF is essential for simplifying ratios and fractions to their lowest terms. For example, the ratio 28:49 can be simplified to 4:7 by dividing both numbers by their GCF, 7.
Beyond the Basics: Exploring Further Concepts
Understanding the GCF opens doors to more advanced mathematical concepts.
1. Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is divisible by both numbers. The GCF and LCM are related by the formula: GCF(a, b) x LCM(a, b) = a x b. Knowing the GCF of 28 and 49 (7) allows you to easily calculate their LCM.
Using the formula: 7 x LCM(28, 49) = 28 x 49. Solving for LCM(28, 49), we find it to be 196.
2. Modular Arithmetic
GCF plays a crucial role in modular arithmetic, a branch of number theory dealing with remainders. It's fundamental in cryptography and other areas of computer science.
Conclusion
This comprehensive exploration answers the initial question: the GCF of 28 and 49 is 7. However, the significance of this seemingly simple calculation extends far beyond a single answer. Understanding the various methods for finding the GCF, its real-world applications, and its connection to more advanced mathematical concepts provides a solid foundation for further mathematical exploration and problem-solving. The GCF is not just a mathematical concept; it's a powerful tool with practical applications in various fields, reinforcing its importance in mathematical education and beyond. Mastering this concept opens doors to a deeper understanding of number theory and its applications in the real world.
Latest Posts
Latest Posts
-
0 008 Is 1 10 Of What Decimal
May 12, 2025
-
How Do Slide Presentations Help Keep The Presenter On Message
May 12, 2025
-
How Many Months Are In Five Years
May 12, 2025
-
How Many Weight Watchers Points In Quinoa
May 12, 2025
-
How Many Pounds Of Pasta For 40 People
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 28 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.