What Is The Greatest Common Factor Of 3 And 6
Arias News
May 11, 2025 · 6 min read
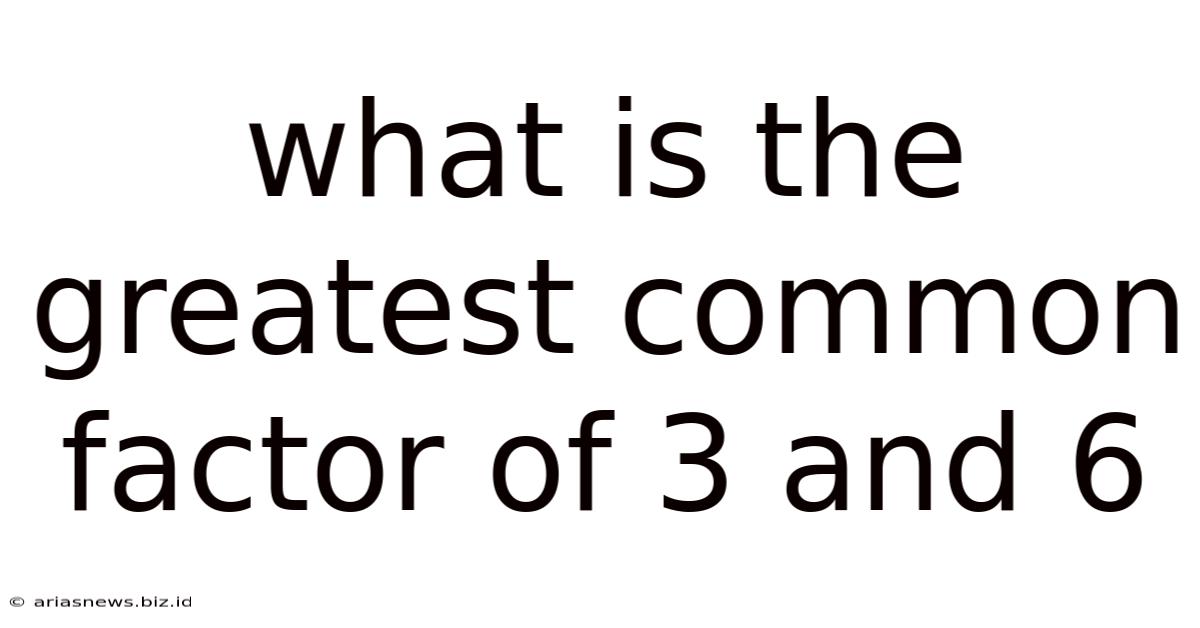
Table of Contents
What is the Greatest Common Factor of 3 and 6? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more advanced mathematical ideas. This article will not only answer the question, "What is the greatest common factor of 3 and 6?", but also explore the broader significance of GCFs in number theory and their practical applications.
Understanding the Fundamentals: Factors and Common Factors
Before diving into the GCF of 3 and 6, let's establish a strong foundation. A factor of a number is a whole number that divides the number evenly, leaving no remainder. For instance, the factors of 6 are 1, 2, 3, and 6. Each of these numbers divides 6 without leaving a remainder. Similarly, the factors of 3 are 1 and 3.
Now, let's consider common factors. These are factors that two or more numbers share. Looking at 3 and 6, we see that both numbers have 1 and 3 as factors. Therefore, 1 and 3 are the common factors of 3 and 6.
Defining the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is simply the largest of these common factors. In our example, comparing the common factors of 3 and 6 (which are 1 and 3), we see that 3 is the largest. Therefore, the greatest common factor of 3 and 6 is 3.
Methods for Finding the GCF: A Practical Approach
While the GCF of 3 and 6 is easily determined through observation, larger numbers require more structured methods. Here are some common techniques:
1. Listing Factors: A Simple, Intuitive Method
This method involves listing all the factors of each number and then identifying the largest common factor. For larger numbers, this method can become cumbersome. Let's illustrate with a different example: Finding the GCF of 12 and 18.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest of these is 6, so the GCF(12, 18) = 6.
2. Prime Factorization: A Powerful Technique
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's find the GCF of 12 and 18 using prime factorization:
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factors are 2 and 3. To find the GCF, we take the lowest power of each common prime factor: 2¹ x 3¹ = 6. Therefore, GCF(12, 18) = 6.
This method is particularly efficient for larger numbers, as it avoids the need to list all factors.
3. Euclidean Algorithm: An Elegant Approach for Larger Numbers
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger values. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's find the GCF of 48 and 18 using the Euclidean algorithm:
- 48 = 2 x 18 + 12 (We divide 48 by 18, the remainder is 12)
- 18 = 1 x 12 + 6 (We divide 18 by 12, the remainder is 6)
- 12 = 2 x 6 + 0 (We divide 12 by 6, the remainder is 0)
When the remainder is 0, the GCF is the last non-zero remainder, which is 6. Therefore, GCF(48, 18) = 6.
The Euclidean algorithm is computationally efficient and forms the basis for many advanced algorithms in number theory and cryptography.
Beyond the Basics: Applications of GCF
The concept of GCF extends far beyond simple arithmetic exercises. It finds crucial applications in various fields:
1. Simplifying Fractions: A Cornerstone of Arithmetic
The GCF is essential for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, to simplify the fraction 12/18, we find the GCF(12, 18) = 6. Dividing both the numerator and denominator by 6 gives us the simplified fraction 2/3.
2. Solving Real-World Problems: Practical Applications
GCF can be applied to solve practical problems involving division and distribution. Imagine you have 12 apples and 18 oranges, and you want to divide them into identical bags with the maximum number of fruits in each bag. The GCF(12, 18) = 6 tells us you can make 6 identical bags, each containing 2 apples and 3 oranges.
3. Number Theory and Cryptography: Advanced Applications
GCF plays a vital role in number theory and cryptography. Concepts like modular arithmetic and the extended Euclidean algorithm, which are built upon GCF principles, are fundamental to modern cryptography techniques used to secure online communication and data.
Expanding Your Knowledge: Related Concepts
Understanding the GCF often opens the door to related concepts in number theory:
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest number that is a multiple of both numbers. The GCF and LCM are closely related; for any two numbers a and b, GCF(a, b) x LCM(a, b) = a x b.
-
Modular Arithmetic: This branch of number theory deals with remainders after division, and GCF plays a crucial role in understanding congruences and solving equations in modular arithmetic.
-
Diophantine Equations: These are equations where only integer solutions are sought. GCF is often instrumental in determining the solvability and finding solutions to certain types of Diophantine equations.
Conclusion: Mastering the GCF and its Applications
The seemingly simple question, "What is the greatest common factor of 3 and 6?" leads us on a journey into the fascinating world of number theory. Understanding GCFs is not just about finding the largest common factor; it's about grasping fundamental concepts that underlie many advanced mathematical and computational techniques with real-world implications. From simplifying fractions to securing online transactions, the GCF is a powerful tool with far-reaching applications. By mastering its calculation and appreciating its broader significance, you equip yourself with a key element in mathematical understanding. So, next time you encounter a GCF problem, remember that it's not just about the answer – it's about the journey of understanding the underlying principles and their profound influence on various mathematical fields.
Latest Posts
Latest Posts
-
Highest Common Factor Of 24 And 56
May 11, 2025
-
1 12 As A Decimal And Percent
May 11, 2025
-
Twice The Sum Of A Number And 5
May 11, 2025
-
Why Are There No Windows In A Jehovah Witness Church
May 11, 2025
-
How To Cook Appleton Farms Spiral Ham
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.