What Is The Highest Common Factor Of 10 And 15
Arias News
May 10, 2025 · 5 min read
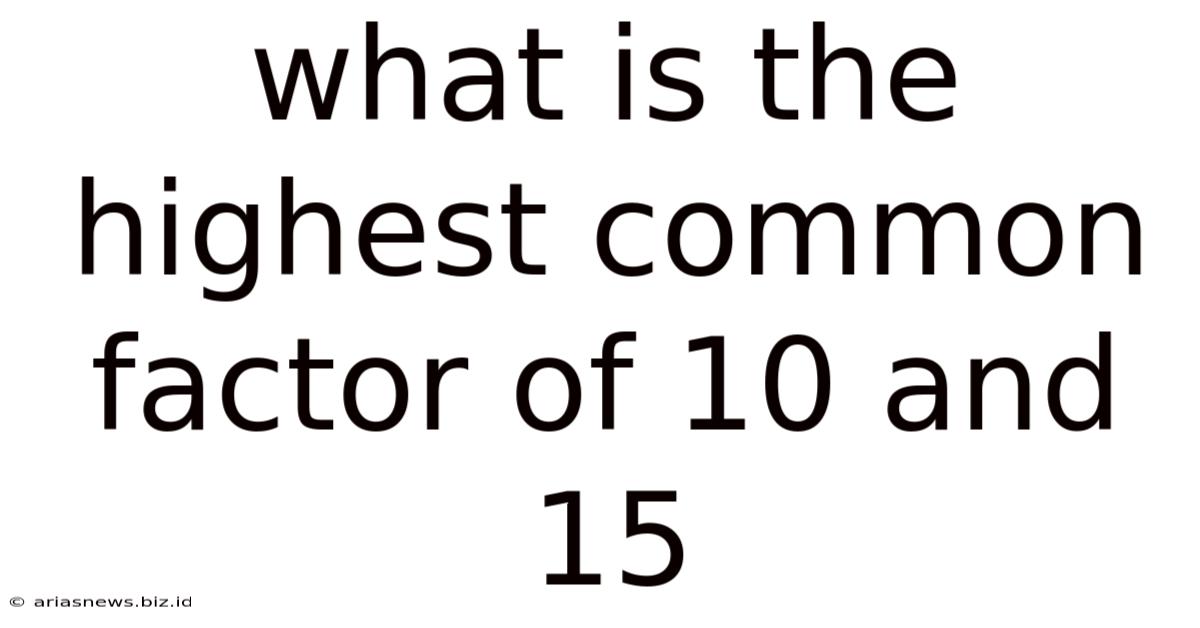
Table of Contents
What is the Highest Common Factor (HCF) of 10 and 15? A Deep Dive into Number Theory
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications in various fields like cryptography, computer science, and even music theory. This article will explore the HCF of 10 and 15 in detail, examining different methods to calculate it and delving into the broader mathematical principles involved. We'll go beyond simply stating the answer, providing a comprehensive understanding of the process and its significance.
Understanding Highest Common Factor (HCF)
Before we tackle the specific case of 10 and 15, let's clarify the definition of HCF. The highest common factor of two or more numbers is the largest positive integer that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The highest of these common factors is 6, so the HCF of 12 and 18 is 6.
Finding the HCF of 10 and 15: Multiple Methods
There are several ways to find the HCF of 10 and 15. We'll explore the most common methods:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
- Factors of 10: 1, 2, 5, 10
- Factors of 15: 1, 3, 5, 15
The common factors of 10 and 15 are 1 and 5. Therefore, the highest common factor (HCF) of 10 and 15 is 5.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The HCF is then found by multiplying the common prime factors raised to their lowest powers.
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
The common prime factor is 5. Therefore, the HCF of 10 and 15 is 5.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially for larger numbers where listing factors becomes cumbersome. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to 10 and 15:
- Start with the larger number (15) and the smaller number (10).
- Subtract the smaller number from the larger number: 15 - 10 = 5
- Now we have 10 and 5. Repeat the process: 10 - 5 = 5
- Now we have 5 and 5. The numbers are equal, so the HCF is 5.
Significance of HCF in Mathematics and Beyond
The HCF is more than just a simple mathematical concept; it has numerous applications in various fields:
1. Simplifying Fractions:
The HCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their HCF. For example, the fraction 15/10 can be simplified by dividing both the numerator and denominator by their HCF, which is 5, resulting in the simplified fraction 3/2.
2. Solving Problems Involving Measurement:
Imagine you have two pieces of wood, one 10 cm long and the other 15 cm long. You want to cut them into smaller pieces of equal length without any waste. The HCF will tell you the length of the largest possible pieces you can cut. In this case, the HCF of 10 and 15 is 5 cm, meaning you can cut each piece of wood into 5 cm long pieces without any waste.
3. Cryptography:
The concept of HCF is fundamental to many cryptographic algorithms. For instance, the RSA algorithm, widely used for secure data transmission, relies heavily on the properties of prime numbers and their HCF. The difficulty of finding the HCF of very large numbers is a cornerstone of the algorithm's security.
4. Music Theory:
Surprisingly, the HCF also finds application in music theory. When determining the intervals between notes, the HCF can be used to find the simplest ratio representing the interval. For instance, the ratio of frequencies of a perfect fifth is 3:2. This is an irreducible fraction because the HCF of 3 and 2 is 1.
5. Computer Science:
In computer science, the HCF is used in various algorithms, including those for finding the least common multiple (LCM), which is closely related to the HCF. Efficient algorithms for calculating the HCF are essential for optimizing the performance of these computer programs.
Beyond the Basics: Exploring LCM and the Relationship with HCF
The least common multiple (LCM) is another important concept closely related to the HCF. The LCM of two or more numbers is the smallest positive integer that is a multiple of each of the numbers. There's a crucial relationship between the HCF and LCM of two numbers:
For any two positive integers 'a' and 'b', the product of their HCF and LCM is equal to the product of the two numbers.
This relationship can be expressed mathematically as:
HCF(a, b) x LCM(a, b) = a x b
Using this relationship, if we know the HCF of two numbers, we can easily calculate their LCM. For 10 and 15, the HCF is 5. Therefore:
5 x LCM(10, 15) = 10 x 15
LCM(10, 15) = (10 x 15) / 5 = 30
So, the LCM of 10 and 15 is 30. This relationship provides a powerful tool for solving problems involving both HCF and LCM.
Conclusion: The Ubiquitous HCF
The seemingly simple task of finding the highest common factor of 10 and 15 opens a window into a rich world of mathematical concepts and their applications. From simplifying fractions to securing data transmission and even creating harmonious music, the HCF's influence is far-reaching. Understanding different methods for calculating the HCF, along with its relationship with the LCM, provides valuable tools for problem-solving across various disciplines. This article aims to solidify your understanding of this fundamental concept, encouraging further exploration of number theory and its fascinating applications.
Latest Posts
Latest Posts
-
How Much Is A Half Of Gallon
May 10, 2025
-
Take The Word Of God With You Lyrics
May 10, 2025
-
How Many Square Feet In 12 Acres
May 10, 2025
-
How Many Pounds Of Rice For 100 People
May 10, 2025
-
0 6 Divided By 10 To The Power Of 2
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Highest Common Factor Of 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.