What Is The Value Of X 55 105
Arias News
May 10, 2025 · 5 min read
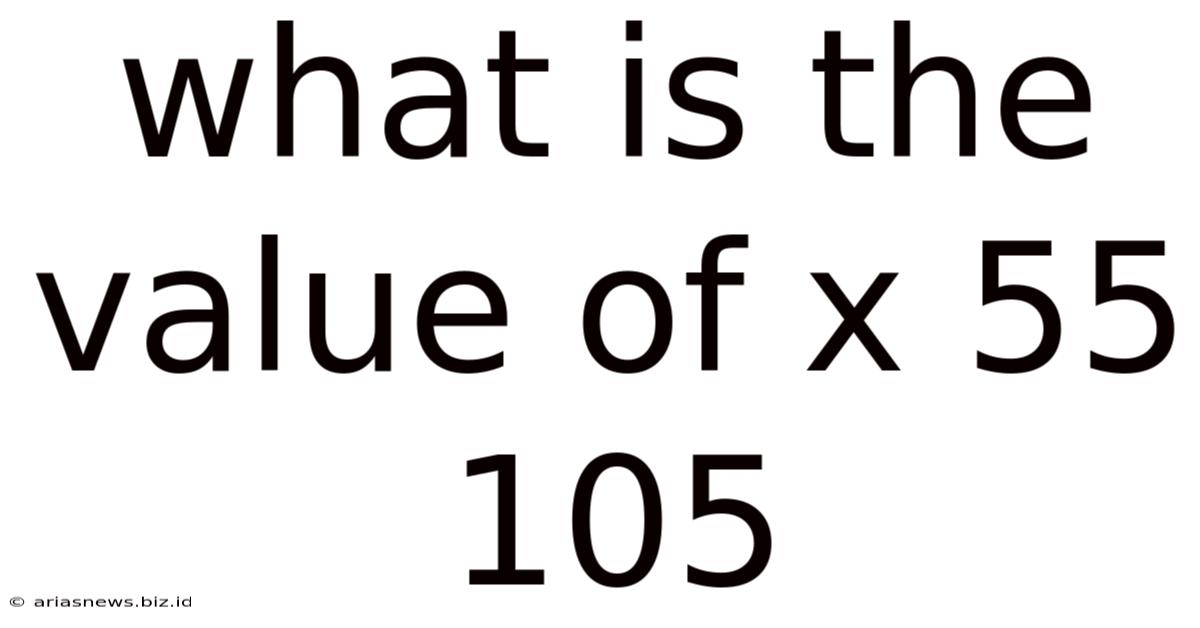
Table of Contents
What is the Value of x: 55, 105, x?
This seemingly simple question, "What is the value of x: 55, 105, x?", delves into the fascinating world of number sequences and pattern recognition. It's not just about finding a solution, but understanding how to find it, and recognizing the underlying mathematical principles. There's no single definitive answer without additional context, highlighting the importance of clearly defining problems in mathematics. However, we can explore several plausible solutions based on different mathematical relationships.
Understanding Number Sequences and Patterns
Before we dive into finding 'x', let's lay a foundation. Number sequences are ordered lists of numbers, often following a specific rule or pattern. Identifying this pattern is crucial to predicting subsequent numbers in the sequence, like finding the value of 'x' in our problem. Several common patterns include:
Arithmetic Sequences
An arithmetic sequence is characterized by a constant difference between consecutive terms. This difference is called the common difference. For example, the sequence 2, 5, 8, 11... is an arithmetic sequence with a common difference of 3.
Geometric Sequences
In a geometric sequence, each term is obtained by multiplying the previous term by a constant value called the common ratio. The sequence 3, 6, 12, 24... is a geometric sequence with a common ratio of 2.
Quadratic Sequences
Quadratic sequences have a second difference that is constant. This means that the difference between consecutive terms forms an arithmetic sequence itself.
Fibonacci Sequences
The Fibonacci sequence is a famous example where each term is the sum of the two preceding terms. It starts with 0 and 1, resulting in the sequence 0, 1, 1, 2, 3, 5, 8, 13...
Potential Solutions for x: 55, 105, x
Let's explore several possibilities for the value of 'x', assuming different patterns in the sequence 55, 105, x:
1. Arithmetic Sequence
Is there a constant difference between 55 and 105? The difference is 105 - 55 = 50. If this is an arithmetic sequence, we would add 50 to 105 to find x:
x = 105 + 50 = 155
Therefore, in an arithmetic sequence, x = 155.
2. Geometric Sequence
Let's see if it's a geometric sequence. We'd need to find the common ratio: 105 / 55 ≈ 1.909. This isn't a whole number, indicating it's less likely to be a simple geometric sequence. However, let's explore further:
x = 105 * 1.909 ≈ 200.45
This solution isn't a neat whole number, making it less likely to be the intended pattern, especially without further context.
3. Quadratic Sequence
For a quadratic sequence, we examine the differences between consecutive terms and the differences between those differences. Let's calculate the first difference:
105 - 55 = 50
To determine if it's quadratic, we need at least one more term. Without that, we cannot definitively conclude whether it is a quadratic sequence.
4. Other Patterns or Relationships
Beyond the standard sequences, there might be other, more complex relationships between 55 and 105 that determine the value of x. This could involve:
- Prime Numbers: Are 55 and 105 related in terms of their prime factorizations? Analyzing their prime factors might reveal a pattern.
- Sums of Digits: Adding the digits of 55 (5 + 5 = 10) and 105 (1 + 0 + 5 = 6) doesn't immediately reveal a clear pattern.
- Specific Mathematical Operations: There could be more intricate mathematical operations (beyond simple addition or multiplication) linking these numbers.
Without additional information or context, pinpointing the exact relationship, and consequently the value of x, is impossible.
The Importance of Context in Solving Mathematical Problems
The ambiguity of this problem highlights the critical role of context in mathematical problem-solving. A complete problem statement should always include:
- Clear Instructions: The question should explicitly state the type of sequence or the relationship between the numbers.
- Sufficient Data: Enough information should be provided to uniquely determine the solution. In this case, having another term in the sequence, or specifying the type of sequence, would greatly improve the problem's clarity.
- Expected Format of the Answer: Should the answer be a whole number, a decimal, or something else?
Expanding the Problem: More Terms and Possibilities
Let's consider extending the sequence. If we had additional terms, we could potentially uncover the underlying pattern more effectively. For instance:
Scenario 1: 55, 105, 155, 205... This would clearly indicate an arithmetic sequence with a common difference of 50.
Scenario 2: 55, 105, 200, 390... This sequence could potentially follow a more complex pattern, perhaps involving a combination of arithmetic and geometric progressions or other non-linear relationships. It might even suggest a function connecting the terms.
Scenario 3: 55, 105, 165, 235... This sequence could be connected by a specific mathematical formula.
Conclusion: The Value of Exploration and Critical Thinking
The question "What is the value of x: 55, 105, x?" serves as a valuable exercise in exploring different mathematical concepts and the importance of critical thinking. While we can't definitively determine 'x' without additional context, the process of investigating various possibilities strengthens our understanding of number sequences, pattern recognition, and the nuances of mathematical problem-solving. It underscores the need for clear problem statements and emphasizes the multiple potential solutions that can emerge when dealing with incomplete information. The pursuit of understanding, even when a definitive answer remains elusive, represents the true value of mathematical exploration. Further investigation into the properties of numbers and the relationships between them is essential for uncovering the underlying patterns. This problem showcases that mathematics, at its core, is about pattern recognition, logical deduction, and exploring different mathematical concepts.
Latest Posts
Latest Posts
-
150 Is 30 Percent Of What Number
May 11, 2025
-
50 Lbs Of Dog Food Is How Many Gallons
May 11, 2025
-
Is The Square Root Of 16 A Rational Number
May 11, 2025
-
How Many 50lb Bags Of Sand In A Yard
May 11, 2025
-
7 Out Of 18 As A Percentage
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 55 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.