Which Interval For The Graphed Function Contains The Local Maximum
Arias News
Apr 02, 2025 · 6 min read
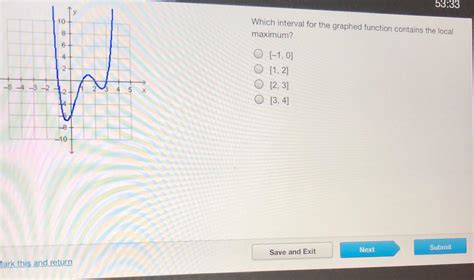
Table of Contents
Which Interval for the Graphed Function Contains the Local Maximum?
Finding local maxima on a graphed function is a crucial concept in calculus and data analysis. A local maximum represents a point where the function's value is higher than its surrounding points within a specific interval. Understanding how to identify these intervals is essential for interpreting trends, making predictions, and solving optimization problems. This article delves into the methods of identifying the interval containing a local maximum on a graphed function, covering various scenarios and providing practical examples.
Understanding Local Maxima
Before we dive into identifying intervals, let's solidify our understanding of what constitutes a local maximum. A local maximum, also known as a relative maximum, is a point where the function's value is greater than the values at nearby points. Crucially, it doesn't need to be the absolute highest point across the entire function's domain; it just needs to be the highest point within its immediate neighborhood.
Key Characteristics of a Local Maximum:
- Higher than surrounding points: The function's value at the local maximum is greater than the values at points immediately to its left and right.
- Not necessarily the absolute maximum: The local maximum might not be the highest point on the entire graph.
- Often associated with a horizontal tangent: In smooth, differentiable functions, the tangent line at a local maximum is horizontal (slope = 0). However, this isn't always the case; consider functions with sharp corners.
Identifying Intervals Containing Local Maxima
The process of identifying the interval containing a local maximum depends on the nature of the function's graph. We'll explore several common scenarios:
1. Smooth, Continuous Functions
For functions that are smooth and continuous (no abrupt jumps or breaks), the local maximum will typically occur where the derivative is zero or undefined.
Steps to Identify the Interval:
- Examine the graph: Visually locate the peak that represents a potential local maximum.
- Determine the x-coordinate: Find the x-value at which this peak occurs.
- Check the neighborhood: Observe the function's behavior immediately to the left and right of this x-value. If the function's value is lower on both sides, you've found a local maximum.
- Define the interval: The interval containing the local maximum will be a small range of x-values centered around the x-coordinate of the peak where the function's value is greater than its neighboring values. The precise interval's boundaries depend on the function's shape and the desired level of precision.
Example:
Consider a function with a local maximum at x = 2. The graph shows the function's value decreasing before x = 2 and increasing after x = 2. The interval containing the local maximum could be (1.5, 2.5), (1.8, 2.2), or any other suitably small range around x = 2. The choice depends on the context and required accuracy.
2. Functions with Discontinuities or Sharp Corners
Functions with discontinuities (jumps) or sharp corners (non-differentiable points) require a slightly modified approach. The derivative might not be zero or undefined at a local maximum in such cases.
Steps to Identify the Interval:
- Examine the graph carefully: Identify the point that visually appears to be a local maximum, even if the function isn't smooth at that point.
- Check the neighborhood: Observe the function's behavior immediately to the left and right of this point. If the function's value is lower on both sides, you have a local maximum.
- Define the interval: Similar to smooth functions, define a small interval around the x-coordinate of the local maximum where the function's value is higher than its surrounding values. The interval may need to be smaller than in the smooth function case to accurately capture the local maximum.
3. Using Calculus (Derivatives)
For functions defined algebraically, calculus provides a powerful method to precisely locate local maxima.
Steps:
- Find the first derivative: Calculate the derivative of the function, f'(x).
- Find critical points: Set the first derivative equal to zero (f'(x) = 0) and solve for x. These are potential locations of local maxima or minima.
- Check the second derivative: Calculate the second derivative, f''(x). Evaluate the second derivative at each critical point.
- If f''(x) < 0, the critical point is a local maximum.
- If f''(x) > 0, the critical point is a local minimum.
- If f''(x) = 0, the test is inconclusive, and further analysis (e.g., the first derivative test) is required.
- Define the interval: Once you've confirmed a local maximum, define an interval around the corresponding x-value where the function's value remains higher than its neighbors.
Example:
Let's consider the function f(x) = -x² + 4x + 5.
- The first derivative is f'(x) = -2x + 4.
- Setting f'(x) = 0 gives -2x + 4 = 0, which solves to x = 2.
- The second derivative is f''(x) = -2. Since f''(2) = -2 < 0, x = 2 is a local maximum.
- The interval containing the local maximum could be (1.5, 2.5), (1.9, 2.1), etc., depending on the level of detail required.
Advanced Techniques and Considerations
- Numerical Methods: For complex functions where analytical derivatives are difficult to obtain, numerical methods (like gradient descent) can approximate the location of local maxima.
- Multiple Local Maxima: Some functions might have multiple local maxima. You'll need to identify and define the interval for each individual local maximum.
- Global Maximum vs. Local Maximum: Remember that a local maximum is not necessarily the global maximum (the absolute highest point on the entire function's domain).
- Context and Application: The choice of interval size depends heavily on the context. In some applications, a wide interval might suffice, while in others, a very narrow interval might be essential.
Practical Applications
Identifying local maxima has widespread applications in various fields:
- Optimization Problems: In engineering, economics, and operations research, finding local maxima (or minima) is critical for optimizing processes and resource allocation.
- Data Analysis: Identifying peaks in data sets (e.g., stock prices, sales figures) can reveal significant trends and patterns.
- Signal Processing: Local maxima detection is crucial for identifying significant events or features in signals, such as in image processing or audio analysis.
- Machine Learning: Many machine learning algorithms rely on finding optimal parameters, often involving the identification of maxima or minima.
Conclusion
Determining the interval containing a local maximum on a graphed function is a fundamental skill with wide-ranging applications. While visual inspection can often suffice for simple functions, more sophisticated techniques involving calculus and numerical methods are necessary for complex scenarios. Understanding the properties of local maxima, coupled with a systematic approach, will enable you to accurately identify these crucial points and gain valuable insights from the data represented by the graphed function. Remember to always consider the specific context and desired level of precision when defining the interval. The accuracy of your interval directly impacts the reliability of any conclusions drawn from your analysis. Remember to always double-check your work and utilize different methods to confirm your findings for enhanced accuracy and reliability. A deeper understanding of these concepts will empower you to effectively analyze functions and draw meaningful conclusions from graphical data.
Latest Posts
Latest Posts
-
Wine Coolers With The Highest Alcohol Content
Apr 03, 2025
-
Greatest Common Factor Of 48 And 64
Apr 03, 2025
-
What Does It Mean To Empathize With A Monster
Apr 03, 2025
-
What Is The Average Iq For A 15 Year Old
Apr 03, 2025
-
Why Might An Aouthor Choose To Use Third Person Narrator
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Which Interval For The Graphed Function Contains The Local Maximum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
