Least Common Multiple Of 4 6 8
Arias News
May 11, 2025 · 5 min read
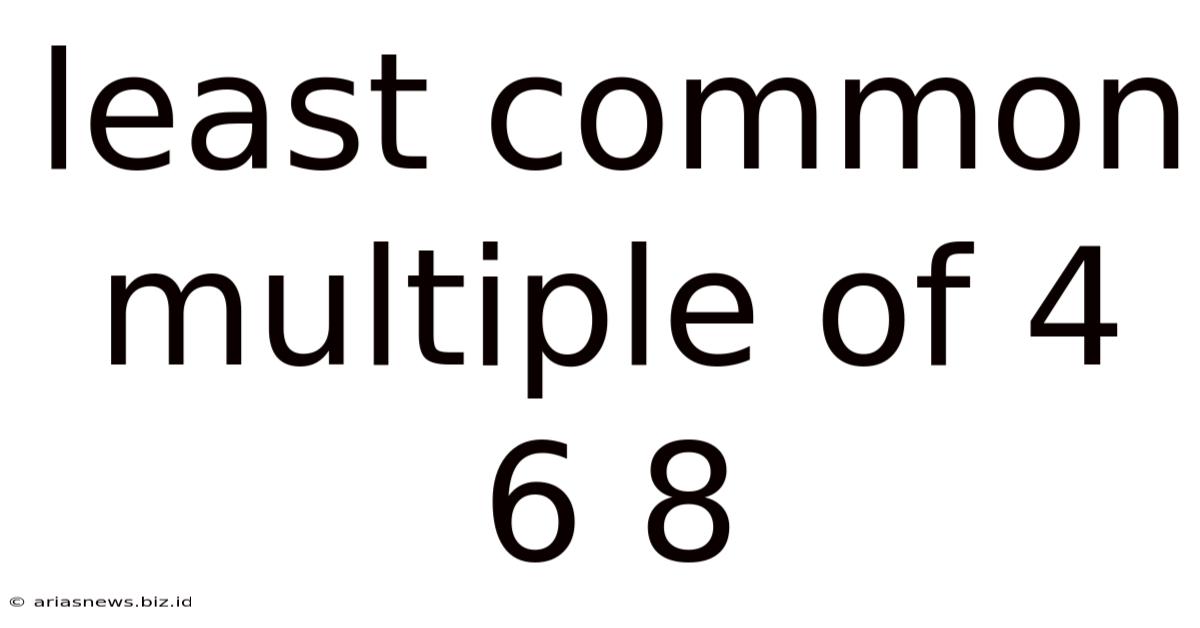
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 8: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in arithmetic and number theory. It represents the smallest positive integer that is a multiple of all the given integers. Understanding how to calculate the LCM is crucial for various mathematical applications, from simplifying fractions to solving problems in algebra and beyond. This comprehensive guide will delve into the methods for finding the LCM of 4, 6, and 8, explore the underlying principles, and provide practical examples. We'll also touch on the broader significance of LCMs in mathematics and beyond.
Understanding Least Common Multiples
Before we dive into calculating the LCM of 4, 6, and 8, let's establish a solid foundation. The LCM is the smallest positive number that is divisible by each of the given numbers without leaving a remainder. For instance, the multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...; the multiples of 6 are 6, 12, 18, 24, 30, 36, 42...; and the multiples of 8 are 8, 16, 24, 32, 40, 48...
The LCM is the smallest number that appears in all three lists.
Method 1: Listing Multiples
The simplest method, particularly for smaller numbers, involves listing the multiples of each number until a common multiple is found. Let's apply this to 4, 6, and 8:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48...
- Multiples of 8: 8, 16, 24, 32, 40, 48...
By examining the lists, we can see that the smallest number that appears in all three lists is 24. Therefore, the LCM of 4, 6, and 8 is 24. This method is effective for small numbers, but it becomes cumbersome and inefficient for larger numbers.
Method 2: Prime Factorization
A more efficient and systematic approach uses prime factorization. This method involves breaking down each number into its prime factors—prime numbers that multiply together to give the original number. Let's factorize 4, 6, and 8:
- 4 = 2 x 2 = 2²
- 6 = 2 x 3
- 8 = 2 x 2 x 2 = 2³
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
To find the LCM, we multiply these highest powers together:
LCM(4, 6, 8) = 2³ x 3 = 8 x 3 = 24
This method is significantly more efficient for larger numbers, as it avoids the tedious process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a formula that links the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes more complex. Let's find the GCD of 4, 6, and 8 using prime factorization:
- 4 = 2²
- 6 = 2 x 3
- 8 = 2³
The common prime factor is 2, and the lowest power is 2¹. Therefore, GCD(4, 6, 8) = 2.
Now, we can use the formula (though it's less straightforward with three numbers): We'll first find the LCM of 4 and 6 using the GCD method, then find the LCM of the result and 8.
- LCM(4, 6) x GCD(4, 6) = 4 x 6
- GCD(4, 6) = 2
- LCM(4, 6) x 2 = 24
- LCM(4, 6) = 12
- Now find LCM(12, 8):
- LCM(12, 8) x GCD(12, 8) = 12 x 8
- GCD(12, 8) = 4
- LCM(12, 8) x 4 = 96
- LCM(12, 8) = 24
While this method works, it's less efficient than direct prime factorization for multiple numbers. The direct prime factorization method remains the most effective for finding the LCM of 4, 6, and 8.
Applications of LCM
The concept of LCM has numerous applications across various fields:
-
Fraction Arithmetic: Finding the LCM of the denominators is crucial when adding or subtracting fractions with different denominators. This allows for the conversion of fractions to a common denominator, facilitating the calculation.
-
Scheduling Problems: LCM is used to solve scheduling problems. For instance, if three buses depart from a station at intervals of 4, 6, and 8 hours, respectively, the LCM will determine when they will all depart at the same time again.
-
Cyclic Patterns: LCM is used to analyze repeating patterns or cycles in various scenarios, like the synchronization of repeating events.
-
Number Theory: LCM is fundamental to many concepts in number theory, including modular arithmetic and the study of divisibility.
-
Music Theory: In music theory, the LCM helps determine the least common period of rhythmic patterns or melodies.
Further Exploration: LCM for Larger Numbers
While the methods discussed above are effective for relatively small numbers, calculating the LCM for larger numbers can be more challenging. For such cases, more advanced algorithms and computational tools may be necessary. However, the underlying principles of prime factorization remain crucial.
Conclusion: Mastering the LCM
Understanding and calculating the least common multiple is a valuable skill in mathematics and related fields. While the listing multiples method is suitable for smaller numbers, prime factorization provides a more efficient and systematic approach, especially for larger numbers. Mastering the LCM calculation empowers you to tackle diverse problems involving fractions, scheduling, and cyclical patterns. The examples and explanations provided in this guide offer a comprehensive understanding of the concept and its applications. Remember, the key is to understand the fundamental principles, choose the most efficient method depending on the numbers involved, and practice regularly to strengthen your skills.
Latest Posts
Latest Posts
-
What Is The Gcf Of 8 And 32
May 12, 2025
-
95 Out Of 100 As A Percentage
May 12, 2025
-
Is A Monitor An Output Or Input
May 12, 2025
-
What Are All The Factors Of 11
May 12, 2025
-
Which Polygon Has An Interior Angle Sum Of 1080
May 12, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.